509. Fibonacci Number
The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), for N > 1.
Given N, calculate F(N).
Example 1:
Input: 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.
Example 2:
Input: 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.
Example 3:
Input: 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
Note:
0 ≤ N ≤ 30.
Solution 1: Basic Recursion
class Solution:
def fib(self, N: int) -> int:
if N == 0:
return 0
if N == 1:
return 1
return self.fib(N - 1) + self.fib(N - 2)
This is the simplest possible solution, which uses recursion. The two base cases are if N == 0 and if N == 1. These are the situations in which we have no more work to do, and we can just return the value of N.
If N is greater that 0 or 1, then we have some extra work to do. We know that fib(N) == fib(N - 1) + fib(N - 2), so we return those numbers in our solution.
This solution works fine and is easy to understand, but if you dig deeper, its inefficiency becomes clear. It’s easier to spot with a visual: here is an image showing the chain of method calls if we try to calculate fib(6).
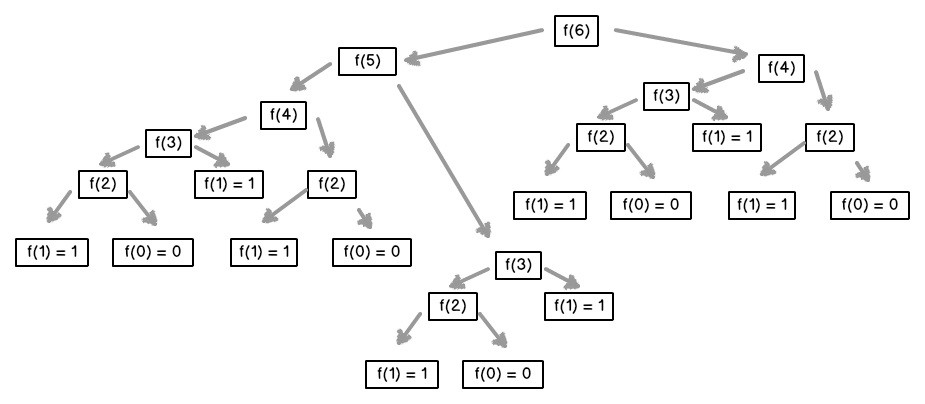
If we look at the general shape of the graph, we can see that each method call creates two more method calls beneath it. This leads to an exponential growth as we move down the tree, and an exponential time complexity of O(2 ^ n).
You can also see that many method calls are calculated multiple times. For instance, we calculate fib(3) three times, and each one creates 4 more methods. If we could simply store the value of fib(3), we could save ourselves a lot of additional computations.
As slow as this solution may be, it is still good enough to pass the Leetcode test cases. However, that is because they only test our code with 0 <= N <= 30. If we even barely increase N to 40, our solution is too slow. So, we look for a faster way.
Solution 2: Memoization
class Solution:
cache = {
0: 0,
1: 1
}
def fib(self, N: int) -> int:
if N not in self.cache:
self.cache[N] = self.fib(N - 1) + self.fib(N - 2)
return self.cache[N]
Memoization is basically a fancy word for storing the result of a method call so that we don’t have to re-calculate it later. In this solution, we create a cache to store the result from each fib call.
This brings our time complexity down to something reasonable, and runs much faster.
Solution 3: Bottom-Up DP
class Solution:
def fib(self, N: int) -> int:
if N < 2:
return N
dp = [0] * (N + 1)
dp[0] = 0
dp[1] = 1
for i in range(2, N + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[N]
“Bottom-Up” in this case means that, unlike with our recursive solution, we start with the lowest values, 1 and 0. We then build our way up to the desired value of N, which is our final solution.
This is the most efficient solution we’ve seen so far. It has time complexity of O(n), as well as space efficiency of O(n). However, there is one more solution that works in O(1) time AND space.
Solution 4: Massive Brain 🤯
# Contributed by LeetCode user mereck.
class Solution:
def fib(self, N):
golden_ratio = (1 + 5 ** 0.5) / 2
return int((golden_ratio ** N + 1) / 5 ** 0.5)
I have no clue how this math actually works, I actually just ripped this solution off of Leetcode. It uses math, so I don’t really understand it. But you can use the Golden Ratio (math thing) to solve this instantly.