867. Transpose Matrix

Given a matrix A, return the transpose of A.

The transpose of a matrix is the matrix flipped over it’s main diagonal, switching the row and column indices of the matrix.

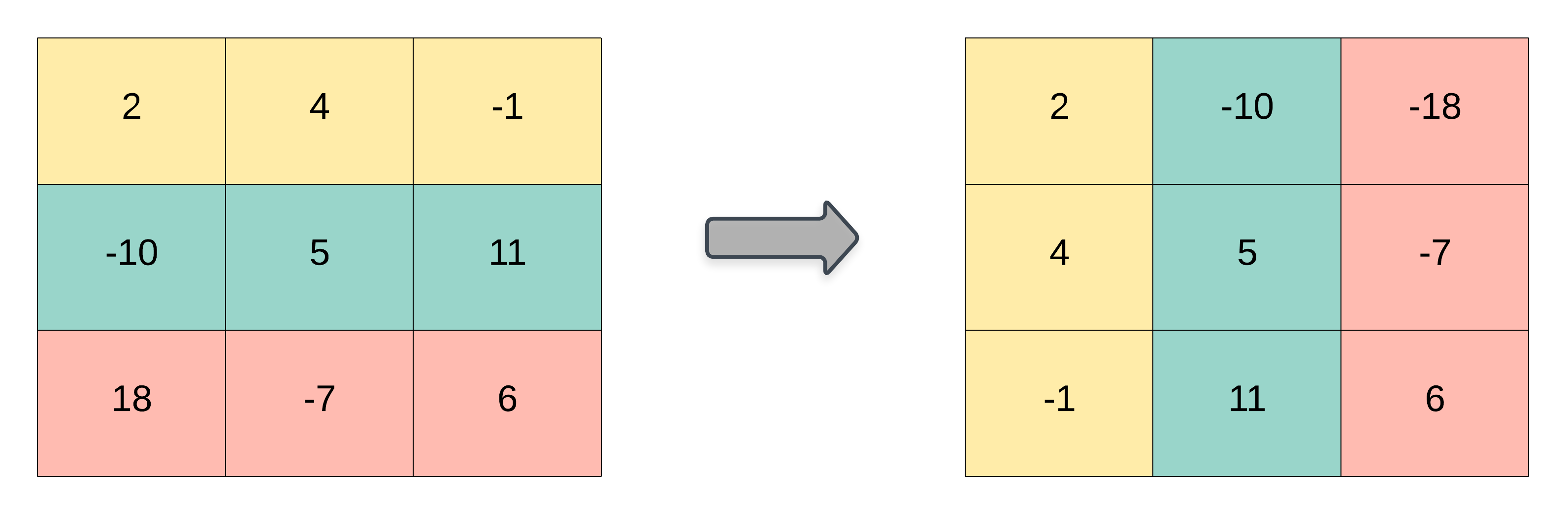
Example 1:

Input: [[1,2,3],[4,5,6],[7,8,9]]
Output: [[1,4,7],[2,5,8],[3,6,9]]

Example 2:

Input: [[1,2,3],[4,5,6]]
Output: [[1,4],[2,5],[3,6]]

Note:

1. 1 <= A.length <= 1000
2. 1 <= A[0].length <= 1000

Solution:

class Solution:
    def transpose(self, A: List[List[int]]) -> List[List[int]]:

        result = [[0] * len(A) for _ in A[0]]

        for r, row in enumerate(A):
            for c, col in enumerate(row):

                result[c][r] = col

        return result

This solution is kind of hard to trace, but it’s very simple in theory. We create a matrix result that is the size of the transposed matrix. We then loop through the given matrix item by item, adding the item to the opposite position in the result.

What this means is that the item at grid[0][2] will end up at position grid[2][0].

Bonus Solution:

class Solution:
    def transpose(self, A: List[List[int]]) -> List[List[int]]:

        return zip(*A)

By using Python’s built in zip method, we can solve this really easily. We feed in all of the rows of A to the method, and it automatically does the work for us.

Try it on Leetcode